Constructed example with some explanations (provided by Ludo Waltman)
The next constructed network was provided by Ludo Waltman (AppendixB.net).For details see AppendixB of the paper:
Ludo Waltman, Nees Jan van Eck, and Ed C.M. Noyons (2010): A unified approach to mapping and clustering of bibliometric networks. Journal of Informetrics, 4, 629-635
Network has 31 vertices and 155 lines. There are different line values (see picture bellow):
- all line values among red vertices are 100
- all line values among yellow vertices (except lines coneected with vertex 31) are 10
- all line values among yellow vertices and vertex 31 are 20
- all line values among green vertices (except lines connected with vertex 31) are 100
- all line values among green vertices and vertex 31 are 50
Resolution parameter r=1
For resolution parameter r=1 Louvain method and VOS Clustering find almost the same partitions into 3 clusters. The difference is in position of vertex 31 (belonging to 'green' cluster in Louvain and 'yellow' cluster in the VOS partition). Visually both partitions seems equally good, but looking at Q and VOSQ values there are small differences that make one partition a bit better than the other.
| Best partition according to Louvain method | Best partition according to VOS Clustering |
| Q(r=1)=0.528331, VOSQ(r=1)=0.809318 | VOSQ(r=1)=0.845447, Q(r=1)=0.527312 |
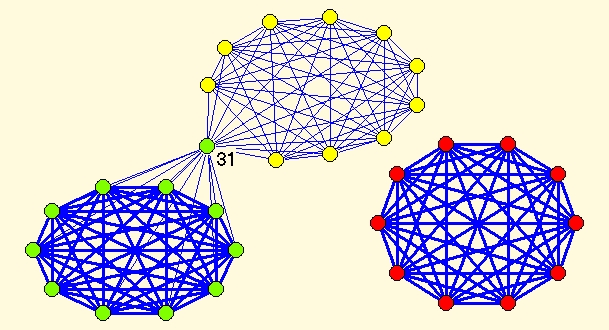 | 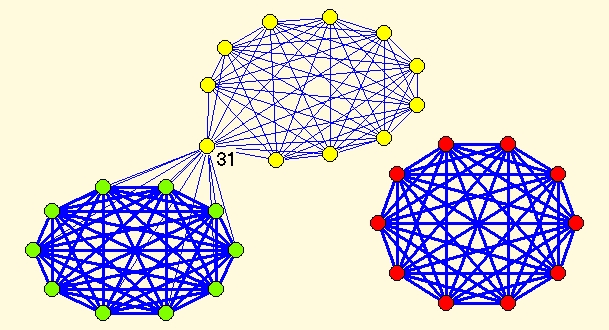 |
Detailed explanation why this happen and why the partition obtained by VOS might be a better one can be found in AppendixB of the paper:
Ludo Waltman, Nees Jan van Eck, and Ed C.M. Noyons (2010): A unified approach to mapping and clustering of bibliometric networks.
Journal of Informetrics, 4, 629-635
Comparing Louvain method and VOS Clustering Back to Pajek and Pajek-XXL Main page.