Visualizing Communities

2. Visualizing communities using 2D Pivot MDS

Pivot MDS fast layout algorithm is implemented in Pajek 3.03 or later.
Pivot MDS enables us to visualize much larger networks than spring embedders.
Networks containing approx. 100.000 vertices can be visualized in few seconds.

Sequence of steps in Pajek

Visualizing using random pivots (without taking communities into account)

Run Layout/Pivot MDS/Random Pivots/2D for layout in plane.
In case of large networks (and small screen) communities obtained occupy too wide area. We can apply Options/Transform/Resize Cluster Area with resize factor smaller than 1 (0.1 seems fine) to make it smaller.

Obtained layout (25069 vertices, 100 random pivots, time needed to compute layout = 1 sec)

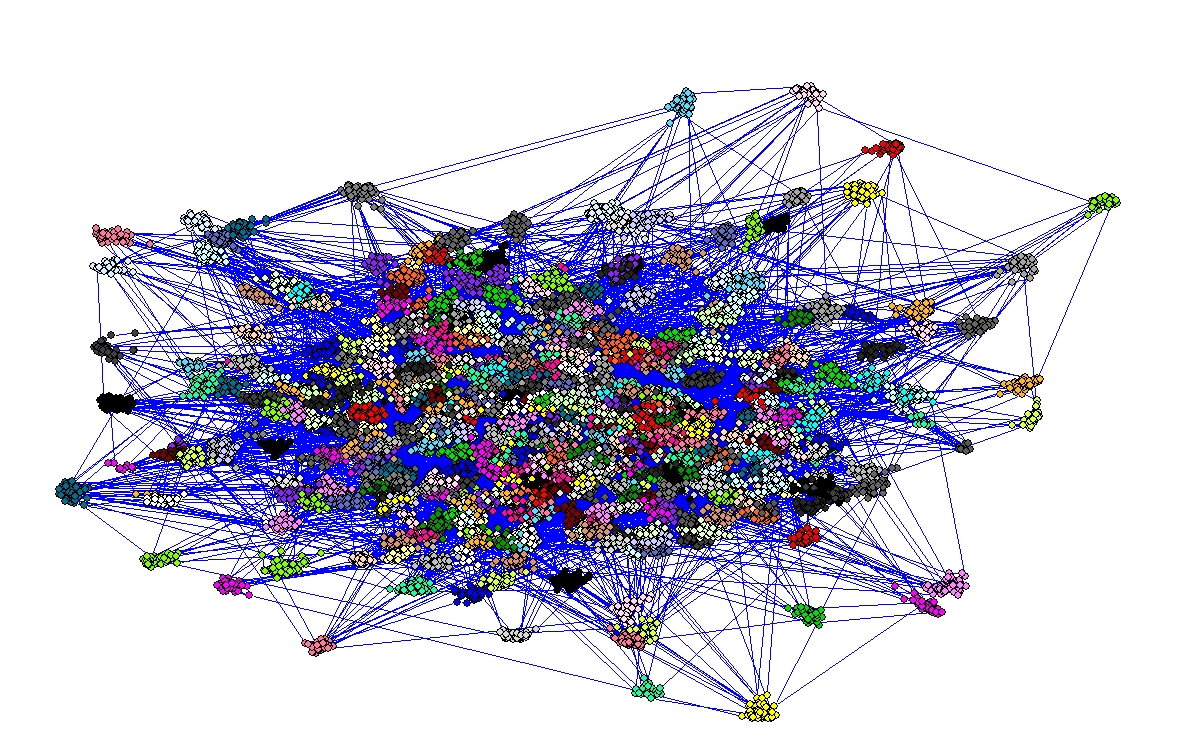
Obtained layout (25069 vertices, 500 random pivots, time needed to compute layout = 15 secs )

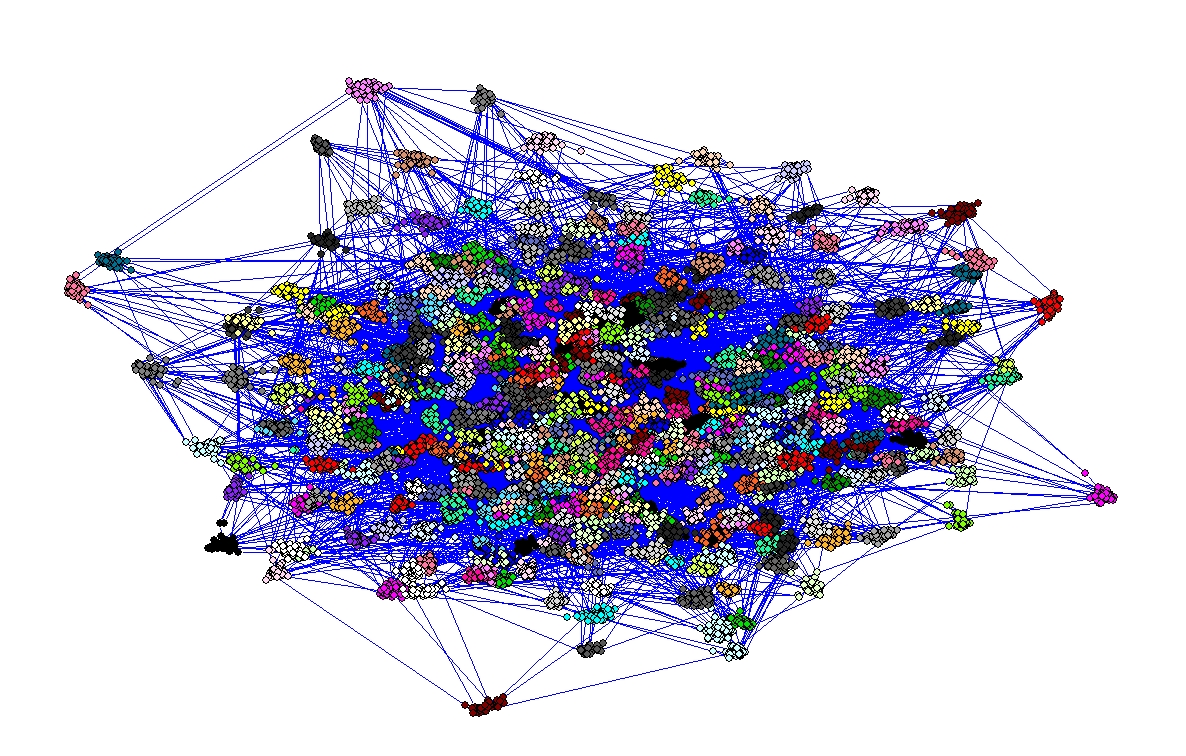
Obtained layout (25069 vertices, 500 random pivots, lines hidden)

Obtained layout (25069 vertices, 500 random pivots, lines hidden, zoomed in)

Visualizing using computed pivots (by taking communities into account)

But we can make it better by taking communities obtained by Louvain method into account. Instead of taking random pivots we can use representatives from communities as pivots. In our case we got 500 communities, and we can randomly select one vertex from each community for its representative:
Apply Partition/Make Cluster/Random Representatives of each Cluster on the obtained community partition.
As result we get a new Cluster with 500 vertices (community representatives).
Then compute layout by running: Layout/Pivot MDS/Pivots from Cluster/2D
Finally apply Options/Transform/Resize Cluster Area to get clusters area smaller.

Obtained layout (25069 vertices, 500 community representatives as pivots, time needed to compute layout = 16 secs)

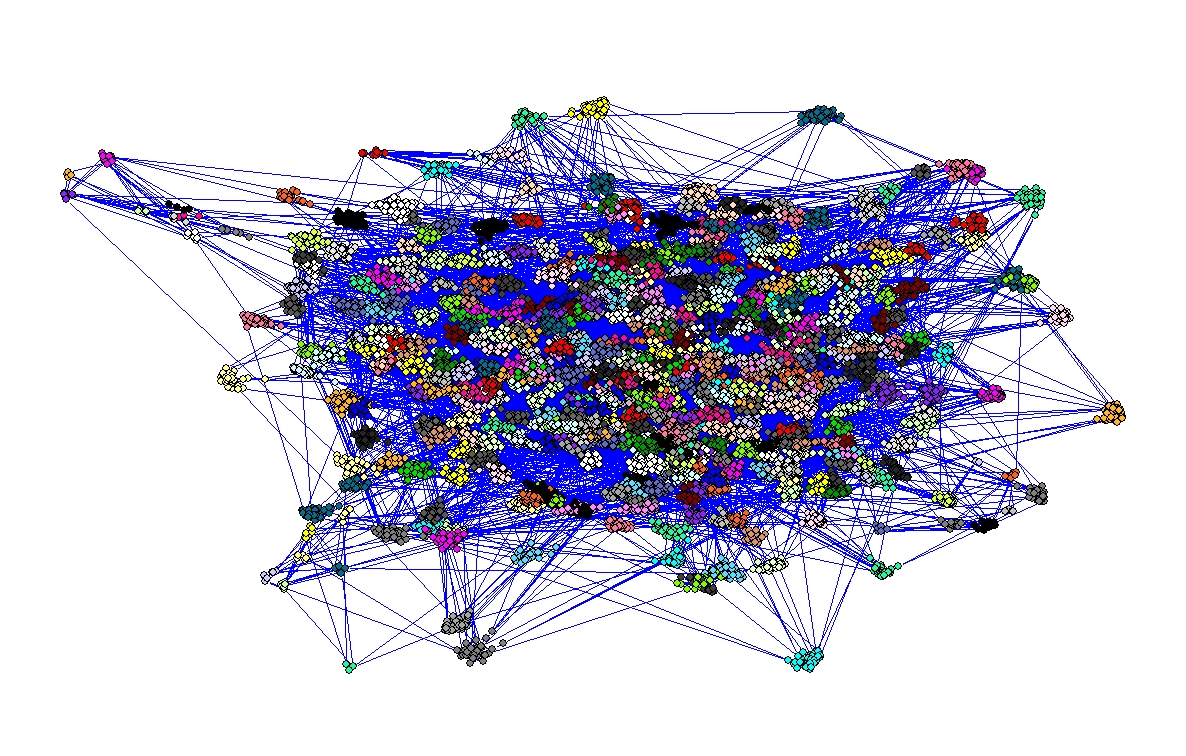
Obtained layout (25069 vertices, 500 community representatives as pivots, lines hidden)

Obtained layout (25069 vertices, 500 community representatives as pivots, lines hidden, zoomed in)

Back to Detecting Communities
Back to Pajek and Pajek-XXL Main page